
Dilatação Associada a Velocidades
No início do século IX já se tinha apurado que é impossível colocar partículas a velocidades iguais ou superiores à velocidade da luz no vácuo e que a velocidade da luz no vácuo é constante.
Einstein, famoso por colocar perguntas pouco convencionais, perguntou-se: o que será que eu vejo caso viaje à velocidade da luz?
Na sua Teoria da Relatividade Restrita, constrói dois postulados, de onde esta parte:
-
As leis da física são aplicáveis a qualquer referencial inercial (referenciais inerciais são referenciais que obedecem à 1ª Lei de Newton, ou seja, que estão em repouso ou em movimento retilíneo uniforme);
-
A velocidade da luz no vácuo é sempre constante e igual a 3*10^8 m/s.

Admitindo este segundo postulado, Einstein sabia que, para isto acontecer, as medições de distância e de tempo não podiam ser iguais para dois observadores
Assim, começou por comparar dois referenciais inerciais, um em repouso e outro num movimento com velocidade constante. Estes seria os pontos de vista de duas pessoas em relação a um comboio, uma externa e um passageiro. Este comboio possui uma fonte de lazer no chão e um espelho no teto.

A partir desta imagem, podemos entender o ponto de vista de cada um dos indivíduos enquanto observam um feixe de luz a sair do lazer e a ser refletido pelo espelho. Na esquerda temos o ponto de vista do passageiro, que vê a luz a subir e descer em linha reta, e na direita temo o ponto de vista da pessoa externa ao comboio, que vê a luz a fazer um "chapéu".
Isto pode ser representado pelo seguinte triângulo:
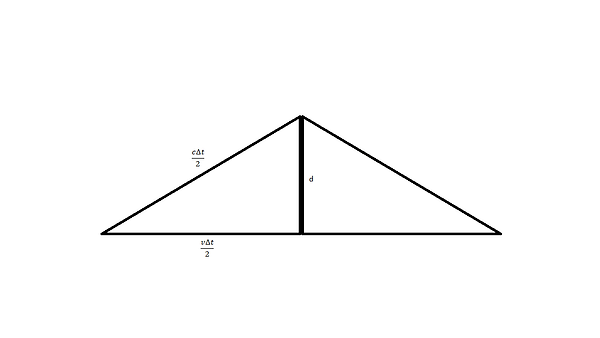
São duas as relações necessárias para se entender e diferença entre os tempos dos dois observadores:
-
A primeira, que é a fórmula da velocidade, quando esta tem módulo constante;
-
A segunda é a relação entre os lados do triângulo acima aplicando o Teorema de Pitágoras.
Por fim, chegamos à relação no final da figura à direita, onde o gama tem o nome de fator de Lorenz
.png)
Tomando um exemplo, imaginemos que vamos a 99% da velocidade da luz. Para nós, o tempo passa 7 vezes mais devagar do que para alguém que está em repouso na Terra.
Para entender melhor estes conceitos, poderá visualizar a seguinte simulação: